This is a 2D CFD simulation of the well known lid-driven cavity flow problem. The reference solution has been taken from Marchi et. al. (2009), The following applications of Kratos are used:
- MeshingApplication
- ExternalSolversApplication
- FluidDynamicsApplication
Case Specification
A one meter square-shaped domain is considered. The fluid parameters are set such that the Reynolds number is 100, thus:
- Density (ρ): 1.0 Kg/m3
- Kinematic viscosity (ν): 0.01 m2/s
The boundary conditions are:
- Bottom, left and right boundaries: No-slip
- Top boundary: v = [1.0,0.0] m/s
- Top left corner: v = [0.0,0.0] m/s
- Top right corner: v = [1.0,0.0] m/s
- Bottom left corner: p = 0.0 Pa
The time step has been set to 0.1 seconds. Regarding the total time, 10 seconds has been proved to be enough to reach a stationary solution.
Results
The problem stated above has been solved with a structured mesh with 200x200 divisions composed by linear triangular elements. The obtained velocity field as well as a centred vertical cross section, comparing the reference solution (solved with a 1024x1024 grid) against the obtained one, are shown below.
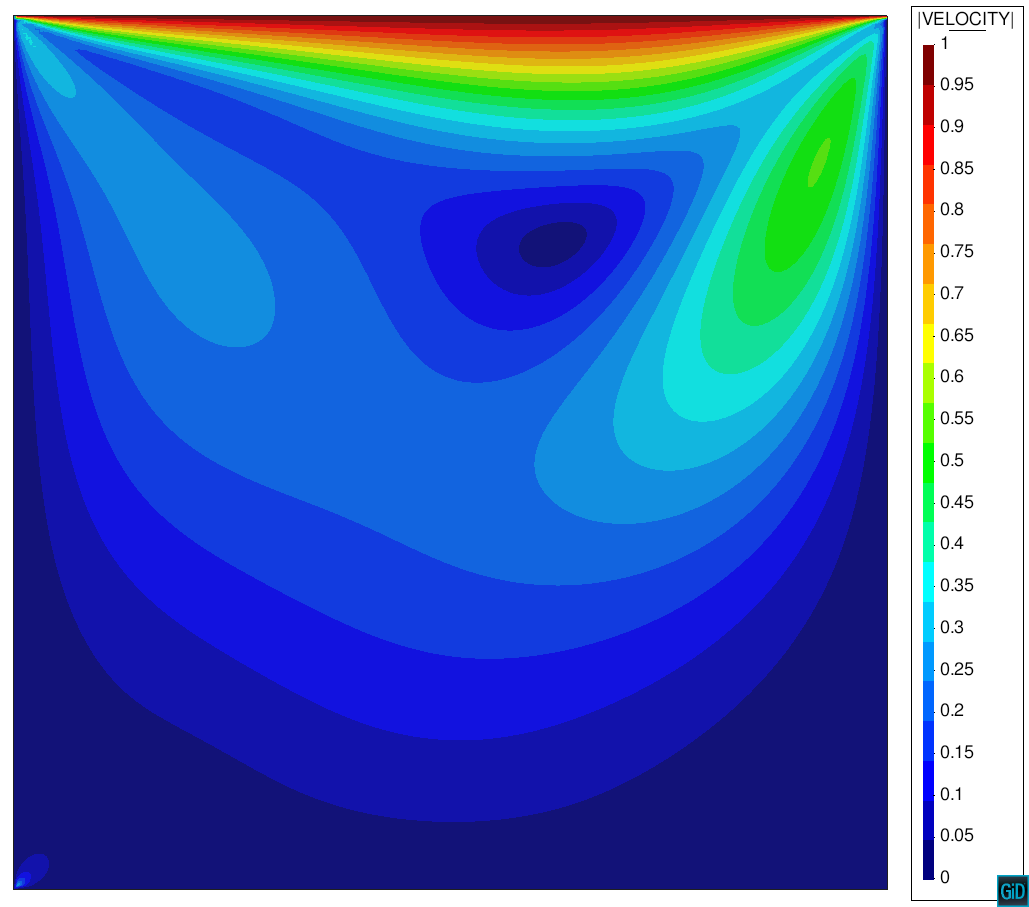
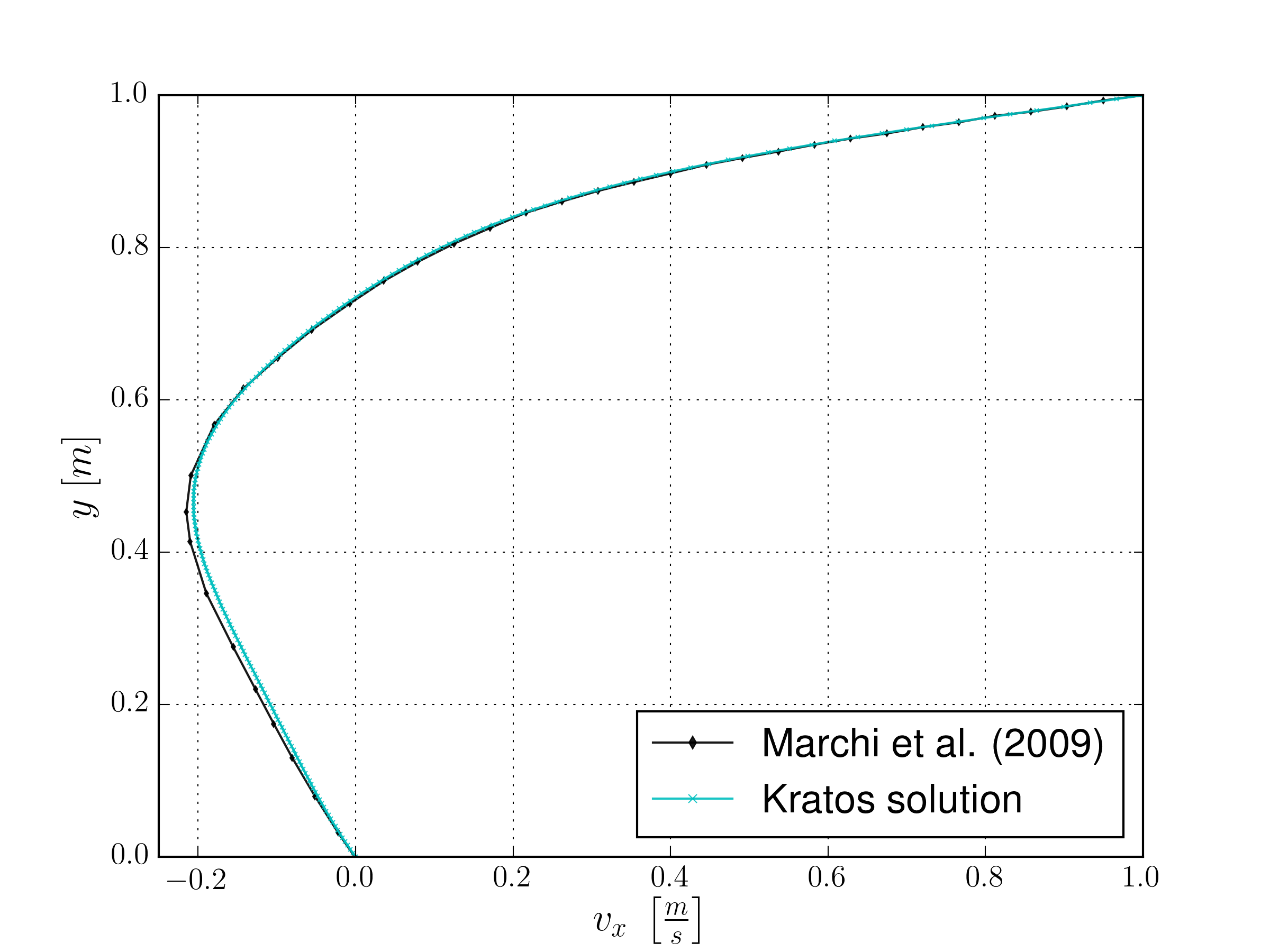
References
Marchi, Carlos Henrique, Suero, Roberta, & Araki, Luciano Kiyoshi. (2009). The lid-driven square cavity flow: numerical solution with a 1024 x 1024 grid. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 31(3), 186-198. https://dx.doi.org/10.1590/S1678-58782009000300004