Problem definition
The linear static orthotropic composite clamped cylinder test considers a cylinder clamped at both ends subject to internal pressure. A cylinder of length a = 20, radius R = 20 and total laminate thickness of h = 1 is subject to a uniform internal pressure of p_0 = (6410/π) [1]. The system is setup as follows:

Problem definition [1]
The laminate is considered in both single and double ply arrangements, with the lamina properties defined as:
- E_1 = 7.5E6,
- E_2 = 2E6
- G_12 = 1.25E6
- G_13 = G_23 = 0.625E6
- ν_12 = 0.25
Due to symmetry only half the cylinder was modeled, while the mesh was refined under the constraint of ‘circumferential divisions = 1.5(axial divisions)’.
The key quantity of interest is the maximum radial displacement of the cylinder, with the reference solution taken from Reference [1].
Results
The following displacement contour of the Kratos thin quad element (mesh = 864 elements) with a 2-ply layup is provided for context.
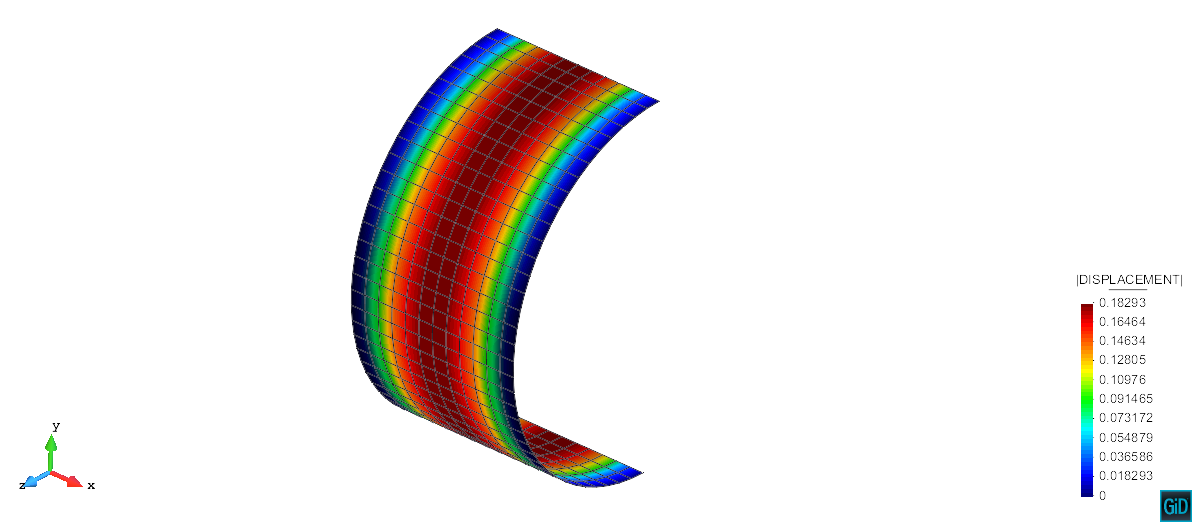
Composite clamped cylinder results: displacement contour of Kratos thin quad element (2 ply layup)
The results of the test for the thin quad and thick triangle Kratos shell elements with a single ply layup are presented below.

Composite clamped cylinder results: single ply layup
The results of the test for the thin quad and thick triangle Kratos shell elements with a double ply layup are presented below.

Composite clamped cylinder results: double ply layup
Both graphs above indicate the thick triangular and thin quadrilateral Kratos shell elements agree with the reference solutions.
References
- Junuthula Narasimha Reddy. Mechanics of laminated composite plates and shells: theory and analysis. CRC press, 2004.