Problem definition
The problem considered is the static geometrically non-linear snap-through of a hinged cylindrical roof under a central point load P = 3000 according to [1]. As per the diagram below, the roof geometry is defined with the parameters: L = 254, R = 2540, theta = 0.1 rad and h = 12.7. The isotropic material is defined by a Young’s modulus of E = 3102.75 and Poisson’s ratio of ν = 0.3.
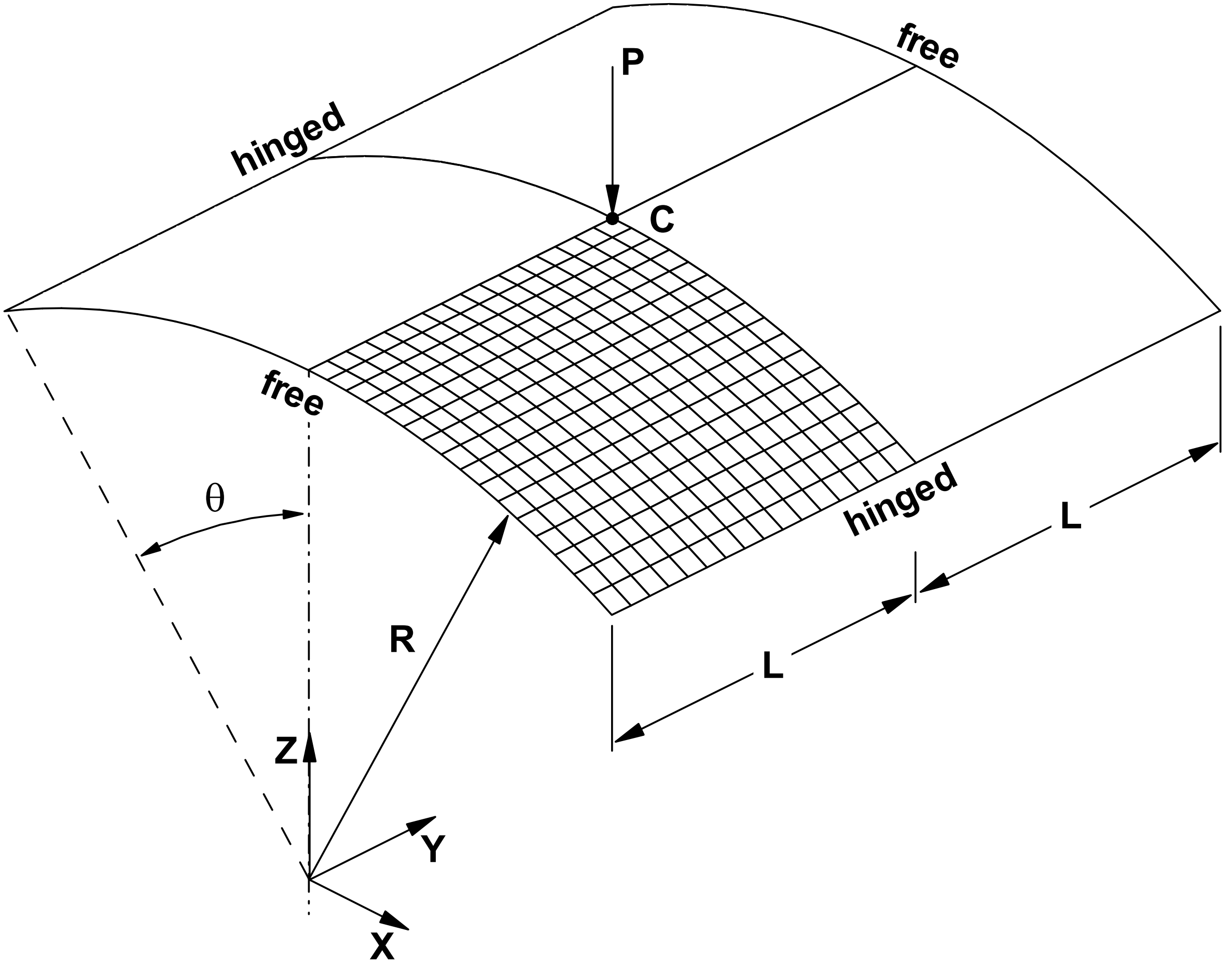
Problem definition [1]
The key result is the vertical point displacement under the point load P in the diagram above, for which the reference equilibrium path according to [1] is plot in the results below.
Results
The following deformation (exaggerated) animation of the Kratos thick quad element (mesh = 256 elements) is provided for context.

Hinged cylindrical roof snapthrough: Deformation of Kratos thick quad element
The results of the test for the thin and thick triangle Kratos shell elements (mesh = 800 elements) are presented below.

Hinged cylindrical roof snapthrough results: triangle elements
The results of the test for the thin and thick quadrilateral Kratos shell elements (mesh = 256 elements) are presented below.

Hinged cylindrical roof snapthrough results: quadrilateral elements
Both graphs above indicate all Kratos triangular and quadrilateral shell elements agree with the reference solution.
References
- K.Y. Sze, X.H. Liu, and S.H. Lo. “Popular benchmark problems for geometric nonlinear analysis of shells”. In: Finite Elements in Analysis and Design 40.11 (2004), pp. 1551 –1569.