Edit me

Introduction

MasterControl is a collection of Controls used by an Algorithm. It is owned by Algorithm and shared among all the ResponseRoutines used by that Algorithm. It does not own any of the Controls, it just links to appropriate Controls found in OptimizationProblem. Thereafter, MasterControl can govern over these Controls.

Working space

As explained above MasterControl will work in the control space and physical space.

Data flow and work flow

It is responsible for converting control space designs (i.e. \(\underline{\hat{\phi}}\)) to physical space designs (i.e. \(\underline{\phi}\)). This is done via the MasterControl::Update method as illustrated in Figure 1. It disassemble the control domain CollectiveExpression (i.e. \(\underline{\hat{\phi}}\)) passed to the master control, to smaller ContainerExpressions control domains (i.e. \(\underline{\hat{\phi}}_1\), \(\underline{\hat{\phi}}_2\)) and then use respective Control to transform to smaller physical domains ContainerExpressions (i.e. \(\underline{\phi}_1\), \(\underline{\phi}_1\)). Then another CollectiveExpression is built aggregating all the smaller physical domains to a larger physical domain (i.e \(\underline{\phi}\)) to get the final physical domain.

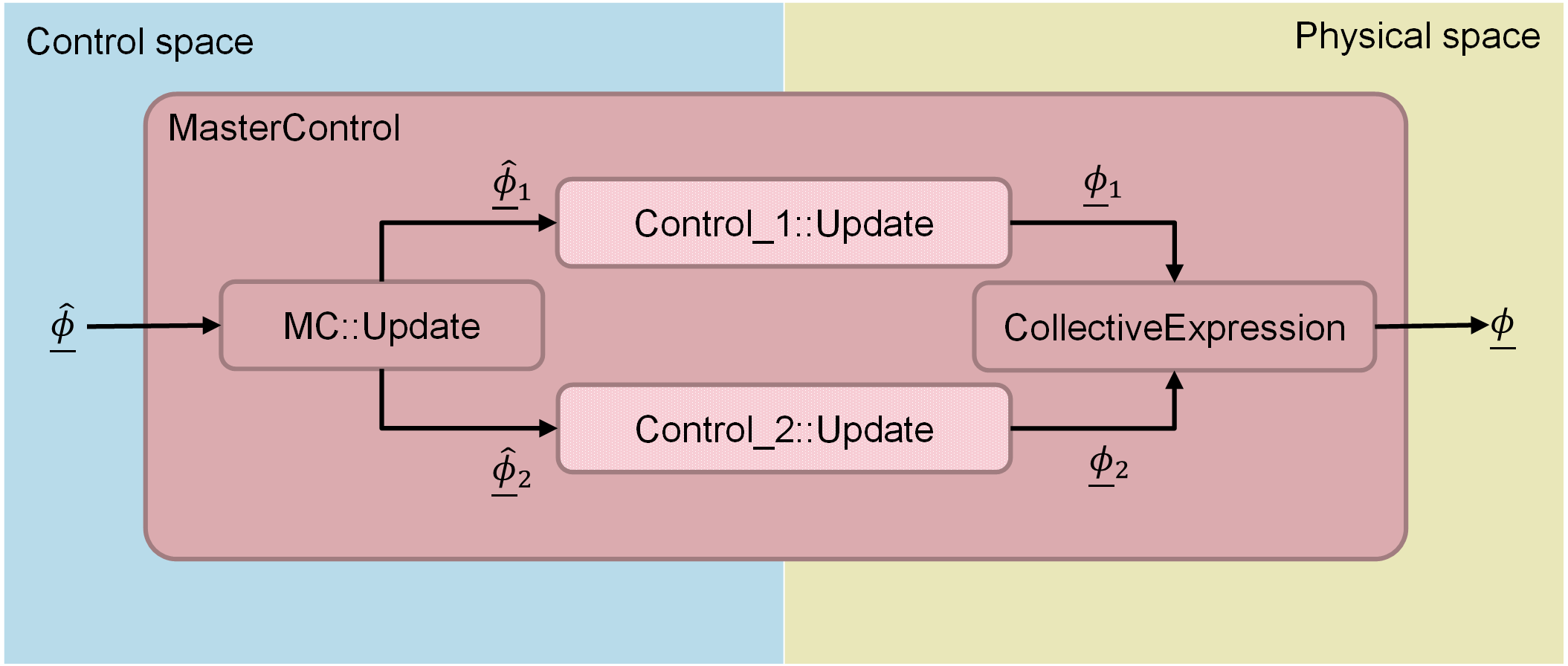
Update method of Master Control

Figure 1: Update method of Master Control

It is also responsible for converting physical domain gradients given in a CollectiveExpression (i.e. \(\frac{dJ_1}{d\underline{\phi}}\)) to the control domain gradients given by again a CollectiveExpression (i.e. \(\frac{dJ_1}{d\underline{\hat{\phi}}}\)) by calling MasterControl::MapGradient as illustrated in Figure 2. There, the passed CollectiveExpression is disassembled to smaller physical domain ContainerExpressions (i.e. \(\frac{dJ_1}{d\underline{\phi}_1}\), \(\frac{dJ_1}{d\underline{\phi}_2}\)). Thereafter, these are passed through their respective Controls to convert to control domain ContainerExpressions (i.e. \(\frac{dJ_1}{d\underline{\hat{\phi}}_1}\), \(\frac{dJ_1}{d\underline{\hat{\phi}}_2}\)). Thereafter, final gradient is computed as a CollectiveExpression by aggregating all the control domain gradients (i.e. \(\frac{dJ_1}{d\underline{\hat{\phi}}}\)).

MapGradient method of Master Control

Figure 2: MapGradient method of Master Control

Notes

  1. MasterControl does not own any of the Controls, but once assigned, these Controls are governed by MasterControl.
  2. There should be only one MasterControl for an optimization analysis.

Source files